

Экспериментальное получение диаграмм растяжения стали
при разных температурах и разработка метода определения температуры стальной проволоки с током.
городской лицей "Единство".
|
| F*10(H) | 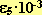 |
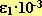 |
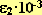 |
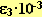 |
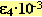 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0,5 | 0,375 | 1,1 | 1,15 | 1,2 | 1,25 |
| 1 | 1,1625 | 1,5 | 1,5 | 1,75 | 1,9 |
| 1,5 | 1,4875 | 1,9 | 2,15 | 2,2 | 2,35 |
| 2 | 1,8 | 2,1 | 2,5 | 2,7 | 2,85 |
| 2,5 | 2,385 | 2,5 | 3 | 3,2 | 3,4 |
| 3 | 2,8 | 3,1 | 3,4 | 3,7 | 3,85 |
| 3,5 | 3,385 | 3,55 | 3,8 | 4,4 | 4,3 |
| 4 | 3,7 | 3,9 | 4,25 | 4,9 | 4,95 |
| 4,5 | 4,15 | 4,25 | 4,55 | 5,3 | 5,45 |
| 5 | 4,6125 | 4,65 | 4,95 | 5,9 | 6 |
| 5,5 | 5,25 | 5,05 | 5,4 | 6,4 | 6,6 |
| 6 | 5,65 | 5,4 | 5,8 | 6,85 | 7,15 |
| 6,5 | 6,1 | 5,85 | 6,3 | 7,3 | 7,85 |
| 7 | 6,575 | 6,3 | 6,7 | 7,7 | 8,5 |
| 7,5 | 7,05 | 6,6 | 7,15 | 8,15 |  |
| 8 | 7,425 | 7,1 | 7,6 | 9 |  |
| 8,5 | 7,875 | 7,45 | 8 | 9,5 |  |
| 9 | 8,4 | 8 | 8,4 | 9,85 |  |
| 9,5 | 8,825 | 8,4 | 8,75 | 10,15 |  |
| 10 | 9,7 | 8,75 | 9,05 | 10,75 |  |
| 10,5 | 10,45 | 9,25 | 9,35 | 11 |  |
| 11 | 11,35 | 9,5 | 9,65 | 11,3 |  |
| 11,5 | 11,8 | 10 | 10 | 11,5 |  |
| 12 |  |
 |
10,4 |  |
 |
| 12,5 |  |
 |
 |
 |
 |
 |
t = -18 градC | t = 40 градC | t = 90 градC | t = 160 градC | t = 270 градC |
Как мы узнали температуру проволоки, по которой течет ток данной величины?
Для этого пришлось придумать и проделать многоходовую комбинацию.
Ход 1.
a) В пробирку без дна поместили спираль из этой проволоки, вставили в нее термометр, который закрыл пробирку с одной стороны, а с другой стороны закрыли пробирку бумажным тампоном, тем самым избавившись от конвекционных потоков, которые возникли бы при пропускании по проволоке электрического тока.
б) Измерили величину тока, вызвавшего едва заметное свечение проволоки (опыт проводился в темноте, с подсветкой шкалы амперметра), она оказалась равной 2,2A.
в) Через достаточно продолжительное время сняли показание термометра, он показал 320 градусов C.
г) Положили тот же термометр на спираль электрической плитки, и на плитку через ЛАТР подали напряжение, при котором спираль начала едва светиться. И в этом случае температура оказалась 320 градусов С.
Ход 2.
Рассчитать температуру проволоки при этой величине тока можно, воспользовавшись законом сохранения энергии за интервал времени, через который проволока (от момента замыкания цепи) начинает светиться.
а) По закону Джоуля -Ленца энергия электрического тока идет на нагревание проводника, на излучение и на конвекцию.
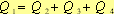 (1),
где:
(1),
где:
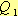 - энергия электрического тока;
- энергия электрического тока;
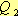 - энергия, идущая на нагревание проводника;
- энергия, идущая на нагревание проводника;
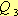 - энергия, уходящая с излучением;
- энергия, уходящая с излучением;
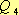 - энергия, уходящая с конвекционными потоками.
- энергия, уходящая с конвекционными потоками.
Определить экспериментально 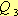 и
и 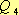 сложно, но сравнив
сложно, но сравнив 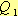 и
и 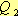 , можно узнать какая доля от энергии тока идет на нагревание проводника, то есть
, можно узнать какая доля от энергии тока идет на нагревание проводника, то есть 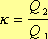 (2),
так как
(2),
так как 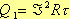 (3),
(3), .gif) (4), где:
(4), где:
 - величина тока, при которой проволока начала светиться;
- величина тока, при которой проволока начала светиться;
R -сопротивление проволоки;
 - время, через которое проволока начинает светиться (от момента замыкания цепи);
- время, через которое проволока начинает светиться (от момента замыкания цепи);
с =460 Дж/(кг*град С) - удельная теплоемкость стали;
m -масса проволоки;
K -коэффициент нагревания;
 - температура проволоки, при которой началось ее свечение;
- температура проволоки, при которой началось ее свечение;
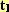 - температура в кабинете.
- температура в кабинете.
Подставляя (3) и (4) в (2) получаем 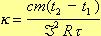 (5).
(5).
Выразим  из равенства (5):
из равенства (5): 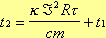 (6).
(6).
R можно узнать из закона Ома: 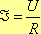 (7), и тогда
(7), и тогда 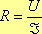 (8),
где U - напряжение на проволоке.
m можно выразить из формулы:
(8),
где U - напряжение на проволоке.
m можно выразить из формулы: 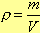 (9)
(9) 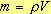 (10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле:
(10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле:
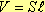 (11),
где:
(11),
где:
S-площадь сечения проволоки;
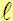 -длина проволоки.
-длина проволоки.
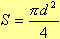 (12), где d - диаметр проволоки.
(12), где d - диаметр проволоки. 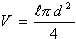 (13),
(13),
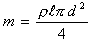 (14).
(14).
Подставляя (8) и (14) в (6), получаем: 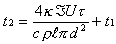 (15).
(15).
В равенстве (15) теперь неизвестно только  и
и 
Ход 3.
Для нахождения  была проведена серия опытов:
была проведена серия опытов:
а) секундомер включали одновременно с замыканием цепи, а выключали его, как только появлялось свечение;
б) цепь размыкали и выжидали время достаточное для остывания проволоки до 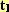 ;
;
в) повторяли 3.а - 3.б. 7раз;
г) рассчитали среднее арифметическое значение  для этого случая, которое оказалось равным 2,5 секунды.
для этого случая, которое оказалось равным 2,5 секунды.
Ход 4.
Для нахождения коэффициента  :
:
а) подставим (8) и (14) в (5), получаем _4pU.gif) (16);
(16);
б) для деформируемой проволоки подставили в (16) следующие данные:
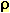 = 7800кг/
= 7800кг/ ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 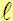 = 0.16 м;
d = 0.27.
= 0.16 м;
d = 0.27.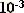 м;
м;
 = 2.4А; U = 7В;
= 2.4А; U = 7В;
 =2.5c;
=2.5c; 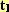 = 13 градусов C;
= 13 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.25.
= 0.25.
Ход 5.
Чтобы убедиться в правильности расчета коэффициента нагревания, повторили Ход 3 и Ход 4 для второй стальной проволоки со следующими данными:
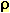 = 7800кг/
= 7800кг/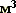 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 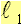 = 0.2 м;
= 0.2 м;
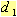 =0.5*
=0.5*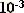 м;
м;
 = 4.6А;
U = 5.5B;
= 4.6А;
U = 5.5B;
 = 15.4c;
= 15.4c;
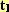 = 20 градусов C;
= 20 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.1.
= 0.1.
Ход 6.
Проверим какую роль играет конвекция на интервале времени  .
.
а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует,
что конвекция в этом случае практически никакого значения не имеет.  =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
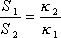 (17), где:
(17), где:
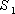 - площадь поверхности проволоки с
- площадь поверхности проволоки с 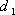 =0.27*10-3 м;
=0.27*10-3 м; 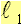 =0.16 м;
=0.16 м;
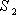 - площадь поверхности проволоки с
- площадь поверхности проволоки с 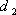 =0.5*10 -3м;
=0.5*10 -3м; 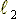 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
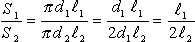 (18)
(18) 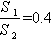 и
и
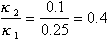 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 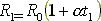 и
и 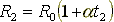 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
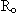 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 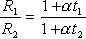 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: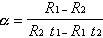 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 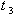 :
:
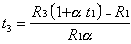 (23),
(23), 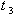 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.
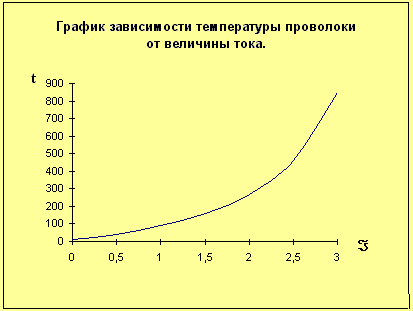
Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.
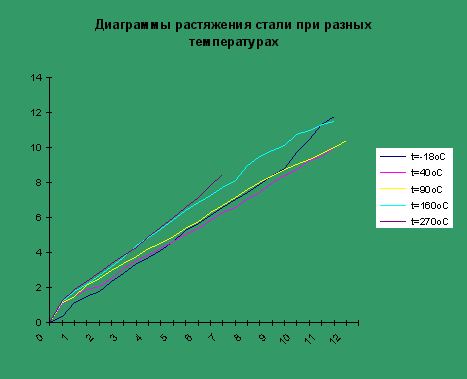
2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
б) Измерили величину тока, вызвавшего едва заметное свечение проволоки (опыт проводился в темноте, с подсветкой шкалы амперметра), она оказалась равной 2,2A.
в) Через достаточно продолжительное время сняли показание термометра, он показал 320 градусов C.
г) Положили тот же термометр на спираль электрической плитки, и на плитку через ЛАТР подали напряжение, при котором спираль начала едва светиться. И в этом случае температура оказалась 320 градусов С.
Ход 2.
Рассчитать температуру проволоки при этой величине тока можно, воспользовавшись законом сохранения энергии за интервал времени, через который проволока (от момента замыкания цепи) начинает светиться.
а) По закону Джоуля -Ленца энергия электрического тока идет на нагревание проводника, на излучение и на конвекцию.
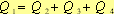 (1),
где:
(1),
где:
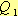 - энергия электрического тока;
- энергия электрического тока;
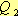 - энергия, идущая на нагревание проводника;
- энергия, идущая на нагревание проводника;
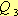 - энергия, уходящая с излучением;
- энергия, уходящая с излучением;
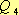 - энергия, уходящая с конвекционными потоками.
- энергия, уходящая с конвекционными потоками.
Определить экспериментально 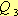 и
и 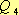 сложно, но сравнив
сложно, но сравнив 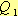 и
и 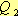 , можно узнать какая доля от энергии тока идет на нагревание проводника, то есть
, можно узнать какая доля от энергии тока идет на нагревание проводника, то есть 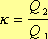 (2),
так как
(2),
так как 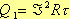 (3),
(3), .gif) (4), где:
(4), где:
 - величина тока, при которой проволока начала светиться;
- величина тока, при которой проволока начала светиться;
R -сопротивление проволоки;
 - время, через которое проволока начинает светиться (от момента замыкания цепи);
- время, через которое проволока начинает светиться (от момента замыкания цепи);
с =460 Дж/(кг*град С) - удельная теплоемкость стали;
m -масса проволоки;
K -коэффициент нагревания;
 - температура проволоки, при которой началось ее свечение;
- температура проволоки, при которой началось ее свечение;
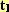 - температура в кабинете.
- температура в кабинете.
Подставляя (3) и (4) в (2) получаем 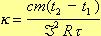 (5).
(5).
Выразим  из равенства (5):
из равенства (5): 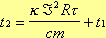 (6).
(6).
R можно узнать из закона Ома: 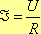 (7), и тогда
(7), и тогда 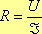 (8),
где U - напряжение на проволоке.
m можно выразить из формулы:
(8),
где U - напряжение на проволоке.
m можно выразить из формулы: 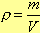 (9)
(9) 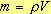 (10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле:
(10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле:
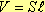 (11),
где:
(11),
где:
S-площадь сечения проволоки;
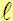 -длина проволоки.
-длина проволоки.
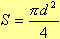 (12), где d - диаметр проволоки.
(12), где d - диаметр проволоки. 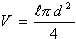 (13),
(13),
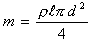 (14).
(14).
Подставляя (8) и (14) в (6), получаем: 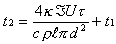 (15).
(15).
В равенстве (15) теперь неизвестно только  и
и 
Ход 3.
Для нахождения  была проведена серия опытов:
была проведена серия опытов:
а) секундомер включали одновременно с замыканием цепи, а выключали его, как только появлялось свечение;
б) цепь размыкали и выжидали время достаточное для остывания проволоки до 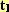 ;
;
в) повторяли 3.а - 3.б. 7раз;
г) рассчитали среднее арифметическое значение  для этого случая, которое оказалось равным 2,5 секунды.
для этого случая, которое оказалось равным 2,5 секунды.
Ход 4.
Для нахождения коэффициента  :
:
а) подставим (8) и (14) в (5), получаем _4pU.gif) (16);
(16);
б) для деформируемой проволоки подставили в (16) следующие данные:
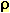 = 7800кг/
= 7800кг/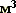 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 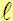 = 0.16 м;
d = 0.27.
= 0.16 м;
d = 0.27.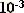 м;
м;
 = 2.4А; U = 7В;
= 2.4А; U = 7В;
 =2.5c;
=2.5c; 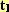 = 13 градусов C;
= 13 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.25.
= 0.25.
Ход 5.
Чтобы убедиться в правильности расчета коэффициента нагревания, повторили Ход 3 и Ход 4 для второй стальной проволоки со следующими данными:
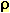 = 7800кг/
= 7800кг/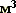 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 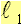 = 0.2 м;
= 0.2 м;
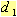 =0.5*
=0.5*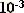 м;
м;
 = 4.6А;
U = 5.5B;
= 4.6А;
U = 5.5B;
 = 15.4c;
= 15.4c;
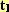 = 20 градусов C;
= 20 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.1.
= 0.1.
Ход 6.
Проверим какую роль играет конвекция на интервале времени  .
.
а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует,
что конвекция в этом случае практически никакого значения не имеет.  =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
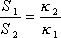 (17), где:
(17), где:
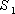 - площадь поверхности проволоки с
- площадь поверхности проволоки с 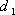 =0.27*10-3 м;
=0.27*10-3 м; 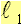 =0.16 м;
=0.16 м;
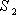 - площадь поверхности проволоки с
- площадь поверхности проволоки с 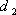 =0.5*10 -3м;
=0.5*10 -3м; 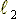 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
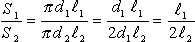 (18)
(18) 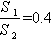 и
и
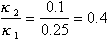 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 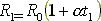 и
и 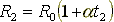 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
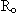 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 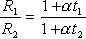 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: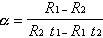 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 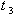 :
:
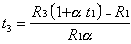 (23),
(23), 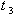 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
а) По закону Джоуля -Ленца энергия электрического тока идет на нагревание проводника, на излучение и на конвекцию.
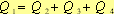 (1),
где:
(1),
где: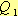 - энергия электрического тока;
- энергия электрического тока;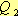 - энергия, идущая на нагревание проводника;
- энергия, идущая на нагревание проводника;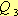 - энергия, уходящая с излучением;
- энергия, уходящая с излучением;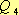 - энергия, уходящая с конвекционными потоками.
- энергия, уходящая с конвекционными потоками.Определить экспериментально
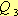 и
и 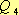 сложно, но сравнив
сложно, но сравнив 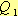 и
и 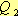 , можно узнать какая доля от энергии тока идет на нагревание проводника, то есть
, можно узнать какая доля от энергии тока идет на нагревание проводника, то есть 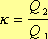 (2),
так как
(2),
так как 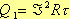 (3),
(3), .gif) (4), где:
(4), где: - величина тока, при которой проволока начала светиться;
- величина тока, при которой проволока начала светиться;R -сопротивление проволоки;
 - время, через которое проволока начинает светиться (от момента замыкания цепи);
- время, через которое проволока начинает светиться (от момента замыкания цепи);с =460 Дж/(кг*град С) - удельная теплоемкость стали;
m -масса проволоки;
K -коэффициент нагревания;
 - температура проволоки, при которой началось ее свечение;
- температура проволоки, при которой началось ее свечение;  - температура в кабинете.
- температура в кабинете.Подставляя (3) и (4) в (2) получаем
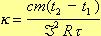 (5).
(5).Выразим
 из равенства (5):
из равенства (5): 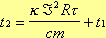 (6).
(6).R можно узнать из закона Ома:
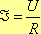 (7), и тогда
(7), и тогда 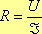 (8),
где U - напряжение на проволоке.
m можно выразить из формулы:
(8),
где U - напряжение на проволоке.
m можно выразить из формулы: 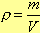 (9)
(9) 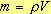 (10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле:
(10),
где нам неизвестен V - объем проволоки, но рассчитать его можно по формуле: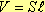 (11),
где:
(11),
где:S-площадь сечения проволоки;
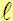 -длина проволоки.
-длина проволоки.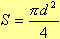 (12), где d - диаметр проволоки.
(12), где d - диаметр проволоки. 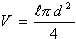 (13),
(13),
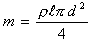 (14).
(14).Подставляя (8) и (14) в (6), получаем:
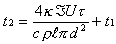 (15).
(15).В равенстве (15) теперь неизвестно только
 и
и 
Ход 3.
Для нахождения  была проведена серия опытов:
была проведена серия опытов:
а) секундомер включали одновременно с замыканием цепи, а выключали его, как только появлялось свечение;
б) цепь размыкали и выжидали время достаточное для остывания проволоки до 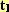 ;
;
в) повторяли 3.а - 3.б. 7раз;
г) рассчитали среднее арифметическое значение  для этого случая, которое оказалось равным 2,5 секунды.
для этого случая, которое оказалось равным 2,5 секунды.
Ход 4.
Для нахождения коэффициента  :
:
а) подставим (8) и (14) в (5), получаем _4pU.gif) (16);
(16);
б) для деформируемой проволоки подставили в (16) следующие данные:
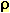 = 7800кг/
= 7800кг/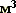 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 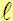 = 0.16 м;
d = 0.27.
= 0.16 м;
d = 0.27.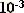 м;
м;
 = 2.4А; U = 7В;
= 2.4А; U = 7В;
 =2.5c;
=2.5c; 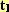 = 13 градусов C;
= 13 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.25.
= 0.25.
Ход 5.
Чтобы убедиться в правильности расчета коэффициента нагревания, повторили Ход 3 и Ход 4 для второй стальной проволоки со следующими данными:
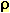 = 7800кг/
= 7800кг/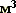 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 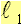 = 0.2 м;
= 0.2 м;
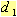 =0.5*
=0.5*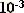 м;
м;
 = 4.6А;
U = 5.5B;
= 4.6А;
U = 5.5B;
 = 15.4c;
= 15.4c;
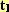 = 20 градусов C;
= 20 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.1.
= 0.1.
Ход 6.
Проверим какую роль играет конвекция на интервале времени  .
.
а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует,
что конвекция в этом случае практически никакого значения не имеет.  =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
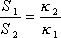 (17), где:
(17), где:
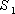 - площадь поверхности проволоки с
- площадь поверхности проволоки с 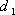 =0.27*10-3 м;
=0.27*10-3 м; 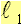 =0.16 м;
=0.16 м;
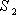 - площадь поверхности проволоки с
- площадь поверхности проволоки с 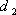 =0.5*10 -3м;
=0.5*10 -3м; 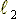 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
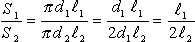 (18)
(18) 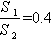 и
и
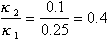 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 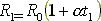 и
и 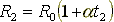 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
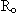 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 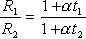 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: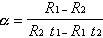 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 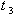 :
:
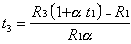 (23),
(23), 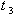 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
 была проведена серия опытов:
была проведена серия опытов:а) секундомер включали одновременно с замыканием цепи, а выключали его, как только появлялось свечение;
б) цепь размыкали и выжидали время достаточное для остывания проволоки до
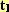 ;
;в) повторяли 3.а - 3.б. 7раз;
г) рассчитали среднее арифметическое значение
 для этого случая, которое оказалось равным 2,5 секунды.
для этого случая, которое оказалось равным 2,5 секунды. Ход 4.
Для нахождения коэффициента  :
:
а) подставим (8) и (14) в (5), получаем _4pU.gif) (16);
(16);
б) для деформируемой проволоки подставили в (16) следующие данные:
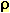 = 7800кг/
= 7800кг/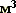 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 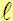 = 0.16 м;
d = 0.27.
= 0.16 м;
d = 0.27.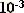 м;
м;
 = 2.4А; U = 7В;
= 2.4А; U = 7В;
 =2.5c;
=2.5c; 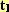 = 13 градусов C;
= 13 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.25.
= 0.25.
Ход 5.
Чтобы убедиться в правильности расчета коэффициента нагревания, повторили Ход 3 и Ход 4 для второй стальной проволоки со следующими данными:
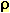 = 7800кг/
= 7800кг/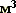 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 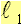 = 0.2 м;
= 0.2 м;
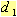 =0.5*
=0.5*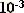 м;
м;
 = 4.6А;
U = 5.5B;
= 4.6А;
U = 5.5B;
 = 15.4c;
= 15.4c;
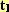 = 20 градусов C;
= 20 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.1.
= 0.1.
Ход 6.
Проверим какую роль играет конвекция на интервале времени  .
.
а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует,
что конвекция в этом случае практически никакого значения не имеет.  =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
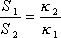 (17), где:
(17), где:
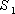 - площадь поверхности проволоки с
- площадь поверхности проволоки с 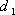 =0.27*10-3 м;
=0.27*10-3 м; 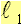 =0.16 м;
=0.16 м;
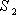 - площадь поверхности проволоки с
- площадь поверхности проволоки с 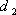 =0.5*10 -3м;
=0.5*10 -3м; 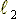 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
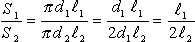 (18)
(18) 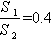 и
и
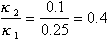 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 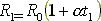 и
и 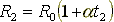 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
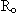 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 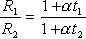 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: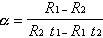 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 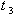 :
:
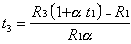 (23),
(23), 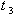 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
 :
:а) подставим (8) и (14) в (5), получаем
_4pU.gif) (16);
(16);б) для деформируемой проволоки подставили в (16) следующие данные:
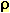 = 7800кг/
= 7800кг/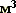 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 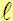 = 0.16 м;
d = 0.27.
= 0.16 м;
d = 0.27.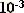 м;
м; = 2.4А; U = 7В;
= 2.4А; U = 7В;
 =2.5c;
=2.5c; 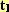 = 13 градусов C;
= 13 градусов C;
 = 320 градусов C;
= 320 градусов C; = 0.25.
= 0.25.
Чтобы убедиться в правильности расчета коэффициента нагревания, повторили Ход 3 и Ход 4 для второй стальной проволоки со следующими данными:
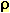 = 7800кг/
= 7800кг/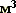 ;
с = 460 Дж/(кг*С);
;
с = 460 Дж/(кг*С); 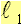 = 0.2 м;
= 0.2 м;
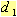 =0.5*
=0.5*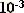 м;
м;
 = 4.6А;
U = 5.5B;
= 4.6А;
U = 5.5B;
 = 15.4c;
= 15.4c;
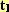 = 20 градусов C;
= 20 градусов C;
 = 320 градусов C;
= 320 градусов C;
и получившийся коэффициент нагревания обозначили  = 0.1.
= 0.1.
Ход 6.
Проверим какую роль играет конвекция на интервале времени  .
.
а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует,
что конвекция в этом случае практически никакого значения не имеет.  =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
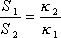 (17), где:
(17), где:
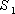 - площадь поверхности проволоки с
- площадь поверхности проволоки с 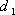 =0.27*10-3 м;
=0.27*10-3 м; 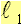 =0.16 м;
=0.16 м;
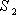 - площадь поверхности проволоки с
- площадь поверхности проволоки с 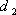 =0.5*10 -3м;
=0.5*10 -3м; 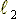 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
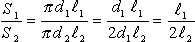 (18)
(18) 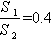 и
и
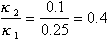 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 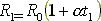 и
и 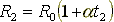 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
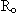 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 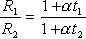 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: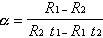 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 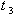 :
:
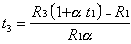 (23),
(23), 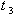 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
 .
.а) повторили Ход 3 и Ход 4 для второй проволоки в вакууме. Из расчета коэффициента нагревания следует, что конвекция в этом случае практически никакого значения не имеет.
 =0.1.
=0.1.
Ход 7.
Если  и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
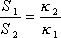 (17), где:
(17), где:
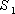 - площадь поверхности проволоки с
- площадь поверхности проволоки с 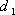 =0.27*10-3 м;
=0.27*10-3 м; 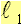 =0.16 м;
=0.16 м;
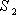 - площадь поверхности проволоки с
- площадь поверхности проволоки с 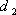 =0.5*10 -3м;
=0.5*10 -3м; 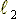 =0.2м;
=0.2м;
 =0.25;
=0.25;
 =0.1.
=0.1.
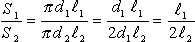 (18)
(18) 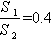 и
и
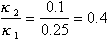 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Ход 8.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 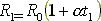 и
и 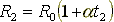 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
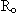 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 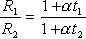 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: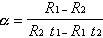 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 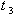 :
:
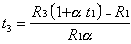 (23),
(23), 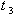 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
 и
и  достоверны, то должно выполняться соотношение:
достоверны, то должно выполняться соотношение:
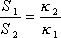 (17), где:
(17), где: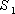 - площадь поверхности проволоки с
- площадь поверхности проволоки с 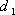 =0.27*10-3 м;
=0.27*10-3 м; 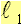 =0.16 м;
=0.16 м;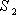 - площадь поверхности проволоки с
- площадь поверхности проволоки с 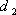 =0.5*10 -3м;
=0.5*10 -3м; 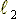 =0.2м;
=0.2м; =0.25;
=0.25; =0.1.
=0.1. 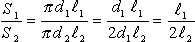 (18)
(18) 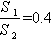 и
и
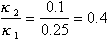 Следовательно,
Следовательно,  =0,25 достоверно.
=0,25 достоверно.
Теперь, зная все величины, мы можем уверенно пользоваться формулой (15).
Ход 9.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
N/N
Свечение
 (A)
(A)
U(B)
R(Oм)
 (c)
(c)
 (C)
(C)
1
еле-еле
2,2
7
2.9
2.5
320
2
слабое
2,6(A)
11
4,2
2,5
540
3
яркое
3
15
5
2,9
990
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 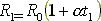 и
и 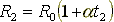 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
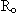 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 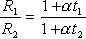 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: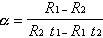 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 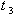 :
:
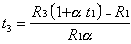 (23),
(23), 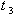 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
При увеличении тока, текущего по проволоке, её температура возрастала и её свечение становилось ярче.
При значениях тока, приведенных в таблице 2, повторялся Ход 3, но под t подразумевалось время, через которое (от момента замыкания цепи) прекращалось изменение свечения, а  рассчитывали по формуле (15) ( смотреть таблицу 2).
рассчитывали по формуле (15) ( смотреть таблицу 2).
Таблица 2
| N/N | Свечение |  (A) (A) |
U(B) | R(Oм) |  (c) (c) |
 (C) (C) |
| 1 | еле-еле | 2,2 | 7 | 2.9 | 2.5 | 320 |
| 2 | слабое | 2,6(A) | 11 | 4,2 | 2,5 | 540 |
| 3 | яркое | 3 | 15 | 5 | 2,9 | 990 |
Ход 10.
Чтобы удостоверится в правильности получившихся температур мы по данным опытов 1 и 2 Хода 9 рассчитали термический коэффициент сопротивления стали, исходя из того, что 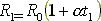 и
и 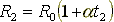 (19) (20), где:
(19) (20), где:
 - термический коэффициент стали;
- термический коэффициент стали;
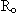 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.
Разделив (14) на (15) получаем: 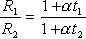 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: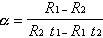 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Ход 11.
Из (21) для первого и третьего опытов выразили 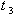 :
:
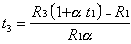 (23),
(23), 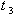 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
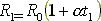 и
и 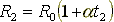 (19) (20), где:
(19) (20), где: - термический коэффициент стали;
- термический коэффициент стали;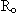 - сопротивление проволоки при температуре равной 0 градусов С.
- сопротивление проволоки при температуре равной 0 градусов С.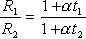 (21);
и выразив
(21);
и выразив  , получаем:
, получаем: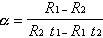 (22). Расчет дает
(22). Расчет дает
 = 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет
= 0.00585 1/K, что близко к табличному (0.006 1/К). Однако расчет  из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
из второго и третьего опытов Хода 9 дал бредовый результат. Значит температура в третьем опыте не достоверна.
Из (21) для первого и третьего опытов выразили 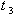 :
:
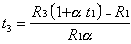 (23),
(23), 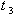 = 850 градусов С.
= 850 градусов С.
Ход 12.
После этого по данным таблицы 3
Таблица 3
 (A)
(A) 0
2.4
2.6
3
t(C)
13
320
540
850
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
После этого по данным таблицы 3
Таблица 3
 (A) (A) |
0 | 2.4 | 2.6 | 3 |
| t(C) | 13 | 320 | 540 | 850 |
был построен график зависимости температуры проволоки от величины тока, текущего по ней.

Ход 13.
По этому графику были определены температуры проволоки при следующих значениях токов (см. таблицу 4).
 (A)
(A) 0
0.5
1
1.5
2
2.5
3
t (C)
13
50
100
160
270
320
850
4. Результаты работы
1. Мы получили диаграммы растяжения стали при разных температурах.

2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
Список литературы:
1."Лабораторный практикум по сопротивлению материалов", А.М.Афанасьев, В.А.Марьин;
2."Сопротивление материалов" - учебник для техникумов , Г.М.Ицкович.
 (A)
(A)1. Мы получили диаграммы растяжения стали при разных температурах.
 |
2. Из сравнения диаграмм видно:
а) с увеличением температуры модуль упругости стали уменьшается, кроме модуля упругости при температуре -18 градусов С;
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
3. Разработали метод определения температуры стальной проволоки с током.
б) при температуре -18 градусов С модуль упругости на интервале нагрузок от 0 Н до 55Н больше, чем у остальных, а затем становится меньше, чем при температуре 40 градусов С, но больше, чем у остальных оставшихся, а при нагрузке 90Н он становится меньше, чем при температуре 16 градусов С, дальше, по мере увеличения нагрузки, становится меньше всех.
Список литературы:
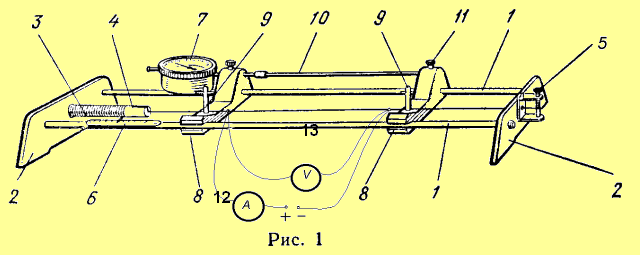
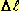 и всякий раз измерять силу упругости F. Для определения величины удлинения проволоки прибор снабжен специальным индикатором малых перемещений (7), позволяющим производить измерения с точностью до 0,01мм.
В описанном приборе измеряется удлинение не всей проволоки, а лишь части, ограниченной двумя ползунками (8), к которым прикрепляют проволоку с помощью винтовых зажимов (9). Такой способ дает возможность избежать искажений, возникающих в опыте вследствие частичного разматывания проволоки в местах ее крепления. На одном из ползунков, расположенном вблизи динамометра, установлен индикатор, а к другому прикреплен стержень (10), который зажимают винтом (11). Стержень имеет
на конце резиновую насадку для соединения его с индикатором. (12)-вольтметр, (13)-амперметр, (+ -)-источник постоянного тока. При растяжении проволоки увеличивается расстояние между ползунками, а стержень, который не меняет своей длинны (он не подвергается действию растягивающей силы ), перемещает штифт индикатора на величину удлинения проволоки.
Проволоку растягивали до разрыва.Изменяли температуру образца так: сначала опыт был проведен на улице при температуре -18 градусов С, а более высокие температуры получали, пропуская различные по величине токи через деформируемую часть стальной проволоки.
и всякий раз измерять силу упругости F. Для определения величины удлинения проволоки прибор снабжен специальным индикатором малых перемещений (7), позволяющим производить измерения с точностью до 0,01мм.
В описанном приборе измеряется удлинение не всей проволоки, а лишь части, ограниченной двумя ползунками (8), к которым прикрепляют проволоку с помощью винтовых зажимов (9). Такой способ дает возможность избежать искажений, возникающих в опыте вследствие частичного разматывания проволоки в местах ее крепления. На одном из ползунков, расположенном вблизи динамометра, установлен индикатор, а к другому прикреплен стержень (10), который зажимают винтом (11). Стержень имеет
на конце резиновую насадку для соединения его с индикатором. (12)-вольтметр, (13)-амперметр, (+ -)-источник постоянного тока. При растяжении проволоки увеличивается расстояние между ползунками, а стержень, который не меняет своей длинны (он не подвергается действию растягивающей силы ), перемещает штифт индикатора на величину удлинения проволоки.
Проволоку растягивали до разрыва.Изменяли температуру образца так: сначала опыт был проведен на улице при температуре -18 градусов С, а более высокие температуры получали, пропуская различные по величине токи через деформируемую часть стальной проволоки.
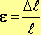 , где:
, где: -начальная длина проволоки ( = 0,2м);
-начальная длина проволоки ( = 0,2м); -относительное удлинение проволоки.
-относительное удлинение проволоки.