---

Назад

---

;Ms Excel

Решение задач по информатике
в электронных таблицах
"Excel"

(Изучение раздела "алгоритмизация" расширенного базового курса информатики в 7-9 классе с использованием электронных таблиц "Excel")

Зайцева Валентина Прокофьевна
Мартыненко Ольга Вячеславовна

Методическое пособие для учителя

Городской методический центр информационных технологий

Мурманск, 2000 год

Решение задач по информатике в электронных таблицах "Excel"1

1 Введение2

2.Программа2

3. Понятие алгоритма3

1-3 Понятие алгоритма 3

2-3 Опорный конспект 3

4 Технология решения задач 6

1-4 Этапы решения задач на ЭВМ (эл.табл.) 6

2-4 Оформление листа решения 6

5 Методы решения задач 7

1-5 Метод последовательных вычислений 7

2-5 Решение задач с условием (методика пpовеpки условия) 12

3-5 Решение задач с повторяющимися действиями 15

* Копирование формул 15

* Функциональные зависимости. 18

* Метод табулирования функций. 19

* Графический метод. 21

* Метод итераций. 23

4-5 Решение задач обработки множеств 24

6 Приложение 1. Встроенные функции “MS Excel 7.0” 24

7 Приложение 2. Примерное тематическое планирование, раздел "Алгоритмы решения задач в электронных таблицах "Excel" 24

8 Литература 24

1 Введение

С появлением тенденции к переходу изучения базового курса информатики в школе от старших классов к среднему звену (7-9 класс) возникают новые проблемы. Это и подбор задач, соответствующих знаниям математики учеников среднего звена, и использование средств и методов преподавания, соответствующих особенностям возрастного восприятия 12-13 летнего ребенка. Авторы попытались подойти к решению этих проблем с новой стороны.

В предложенном пособии рассматривается методика решения большинства задач из курса информатики по технологии обработки числовой информации. Проще говоря, там, где обычно применялся язык программирования, используется только электронная таблица. Идея не новая, но авторы постарались представить эти методы в понятном для школьника виде и предлагают использовать их в школьном курсе информатики.

Использование предлагаемой методики позволит разделить обучение алгоритмическому решению задач на две части. Сначала ребята осваивают и придумывают алгоритмы решения задач, пользуясь только электронными таблицами, не отвлекаясь на изучение синтаксиса языка программирования. Основной целью курса информатики является развитие умения решать задачи, и этому умению следует уделить больше внимания. К записи алгоритмов на языке программирования можно приступить на втором этапе, или вообще изучать язык программирования не в базовом курсе, а в старших классах, в курсе предпрофессиональной подготовки или спецкурсе.

Особенно хочется обратить внимание читателя на классификацию задач. Авторами предложена наиболее естественная (по нашему мнению) классификация, которая отличается от общепринятой терминологией. Кроме того, авторы считают необходимым разделять текстовые задачи и упражнения. Упражнением будем называть задание, где решение уже формализовано, т.е. существует формула, используемая для получения ответа. Текстовые задачи требуют от ученика проделать этап формализации решения самостоятельно.

В курсе информатики именно на отработку умения формализовать способ решения не отводится достаточно времени, а этот вопрос очень важен. В отличие от курса математики, где ребята в 7-9 классе часто знакомятся с одним, двумя алгоритмами решения задач и много часов решают упражнения по известному алгоритму, причем от них не требуется описание самого алгоритма в какой-либо формализованной системе понятий, в курсе информатики к каждой задаче требуется придумать свой алгоритм, что требует существования развитых операциональных способностей мышления.

Значительной особенностью данной методики является высокий уровень наглядности. Работая непосредственно с компьютером, в таблице ученик видит сразу и условие задачи, и начальные данные, и формализацию решения. К уроку можно подготовить файл таблицы, содержащий схему или иллюстрацию к задаче (функция рисования существует). Такой уровень наглядности недоступен при изучении языка программирования.

Пособие построено в соответствии с той частью программы расширенного базового курса, по которой ученики должны изучить раздел "Алгоритмизация". Не все вопросы этого раздела включены в эту брошюру. Мы исключили ту информацию, которая достаточным образом рассмотрена во многих изданиях, например, начальные приемы работы с электронной таблицей. Применение языка программирования, как второй этап обучения алгоритмическому решению задач, мы не рассматриваем вообще, хотя не исключаем его из полной программы базового курса. В каждом разделе рассматривается решение одного упражнения и одной или двух текстовых задач.

Приводится соответствующая часть программы. Полная программа 8 класса рассчитана на 68 часов, причем на изучение возможностей электронных таблиц отводится всего 6 часов, так как предполагается, что начальные навыки работы с таблицей у школьника уже есть в соответствии с программой 7 класса.

2 Программа

расширенного базового курса, раздел "Алгоритмы решения задач в электронных таблицах "Excel"

8 класс, 40 часов

Понятие алгоритма (повторение), 2 часа. Понятие алгоритма. Свойства алгоритмов, исполнители алгоритмов. Способы записи алгоритмов. Формальное исполнение алгоритмов. Основные алгоритмические конструкции. Вспомогательные (подчинённые) алгоритмы.

Возможности электронных таблиц "Excel", 6 часов. Назначение и устройство электронной таблицы. Типы данных. Заполнение и редактирование таблицы. Копирование данных. Пошаговое копирование. Расчет по формулам. Встроенные функции. Копирование формул. Форматирование таблицы.

Технология решения задач, 2 часа. Этапы решения задач на ЭВМ. Формализация решения. Оформление листа решения.

Методы решения задач, 26 часов. Метод последовательных вычислений (4 часа). Метод проверки условия. Команда ветвления (4 часа). Решение задач с повторяющимися действиями. Реализация циклических вычислений (4 часа). Функциональные зависимости. Табулирование функций. Графический метод. Метод итераций (4 часа). Обработка множества элементов таблицы (4 часа). Комбинированные задачи. Реализация вспомогательного алгоритма (6 часов).

Расширенные возможности электронных таблиц "Excel", 4 часа. Связывание документов (листов, файлов). Импорт и экспорт данных.

Требования к знаниям и умениям учащихся.

Учащиеся должны знать: понятие алгоритма, свойства алгоритма, базовые алгоритмические конструкции, способы редактирования и вычислений электронной таблицы, этапы решения задач на ЭВМ, методы решения задач в электронной таблице.

Учащиеся должны уметь: формализовать решение задач различных типов (с последовательными действиями, с условием, с повторяющимися действиями, обработки множеств), построить алгоритм решения задачи базового уровня, оформить лист решения в электронной таблице, построить сетку вычислений по заданному алгоритму.

3 Понятие алгоритма

1-3 Понятие алгоритма

Определение 1.

Алгоритм – это система точных и понятных предписаний о содержании и последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа.

Определение 2.

Алгоритм – это правило, предписывающее последовательность действий над входной информацией и приводящее к результату.

Правило должно обладать дискретностью, массовостью, определенностью, конечностью, понятностью и результативностью.

Свойства алгоритмов:

Дискретность – процесс решения разбивается на ряд последовательных предписаний.

Понятность – представление алгоритма в виде текста, понятного для исполнения.

Определенность – получение одинакового результата каждым исполнителем, которому понятен алгоритм.

Массовость – справедливость алгоритма для различных наборов исходных данных.

Конечность – количество последовательных действий не является бесконечным, их можно посчитать.

Результативность – после точного выполнения всех предписанных действий непременно должен быть получен результат за конечное число шагов.

Как правило, текстом, понятным для компьютера, является программа, разработанная на одном из языков программирования. Также понятной для компьютера является сетка расчетов в электронной таблице, если она правильно организована.

2-3 Опорный конспект

Запишите пропущенные слова

Кибернетика - это наука об управлении различными системами.

Алгоритмизация - общий метод кибернетики, главное в решении задач на ЭВМ.

_______________ - это правило, предписывающее последовательность действий над входной информацией и приводящее к результату.

А_________________ решения задачи на ЭВМ:

постановка задачи;

построение математической модели;

разработка _________________;

реализация __________________ на ЭВМ;

анализ результатов.

Таблица № 1

Свойства __________	Пример выполнения св-ва	пример невыполнения св-ва
дискретность	казнить нельзя, помиловать!	казнить нельзя помиловать
понятность	инструкция по-русски и с картинками	инструкция на общеафриканском языке
определенность	на дубе ларец, в ларце утка, в утке яйцо, в яйце игла, в игле смерть Кащея	поди туда, не знаю куда, принеси то, не знаю что
массовость	Каждой дочери отец привез по дорогому подарку.	принц мог жениться только на настоящей принцессе
конечность	Мама сварила отличную кашу в горшочке.	каша уже заполнила все улицы, а горшочек все варил кашу
результативность	мышка хвостиком вильнула, яйцо и разбилось	баба била-била, не разбила

Напишите название свойства, соответствующее каждому определению.

_________________ - описание процесса решения на языке исполнителя.

_________________ - алгоритм дает правильное решение при различных наборах начальных данных.

_________________ - процесс решения разбит на отдельные шаги.

_________________ - запись алгоритма четкая, полная, ясная.

_________________ - задача решается за известное количество шагов.

_________________ - алгоритм приводит к решению задачи.

Возможности электронных таблиц "Excel"

Электpонная таблица является удобным инстpументом для пpедставления, отобpажения и пpеобpазования инфоpмации.

Перечислим основные понятия и действия, возможные в электронной таблице Excel.

Элементы структуры электронной таблицы: ячейка, строка, столбец, блок ячеек, лист.

Типы данных: числа, текст, формулы, даты.

Адреса ячеек: абсолютный ($А$3) и относительный (А3).

Активная ячейка: та, в которой установлен курсор.

Редактирование данных и формул: содержимое активной ячейки всегда отражается в строке функций. Установите курсор в строку функций, внесите изменения и нажмите Enter.

Копирование данных: [Ctrl+C] – разместить данные в буфер обмена,
[Ctrl+V] – вставить данные из буфера обмена.

Пошаговое копирование: если записать в двух ячейках два разных числа (разность между числами – шаг), затем выделить эти две ячейки, то можно получить ряд чисел в других ячейках с заданным шагом протаскиванием "мышки". Например: 1 и 2, шаг 1, получим копированием ряд 3, 4, 5, 6, и т.д.

Вычисления по формулам: формула начинается всегда со знака « = ». В формуле можно использовать числа и адреса ячеек.

Копирование формул: относительные адреса ячеек меняют свое значение при копировании формул, абсолютные адреса не меняют значения.

Использование встроенных функций: в формуле можно использовать стандартные функции (математические, статистические, логические и другие). Функцию и необходимые аргументы можно просто набрать на клавиатуре или использовать для написания мастер функций ( f_x ). См. приложение 1.

Форматирование таблицы: Для листа или блока ячеек можно определить тип данных и параметры заданного типа данных путем форматирования. Сначала выделите блок ячеек, используйте меню "Формат" - "Ячейки".

Экспоненциальная запись числа: число может быть записано в виде
334576 = 3.345Е+5. Знак Е обозначает "10 в степени", число +5 – это степень 10. Для того, чтобы привести число к обычному виду, добавим 5 знаков после точки: 3.345Е+5 = 3.345 * 100000 = 334500
Такая запись используется для больших чисел.

Построение диаграмм: для наглядного представления данных можно построить диаграмму (гистограмму, круговую, линейный график и др.) при помощи мастера диаграмм. Редактирование диаграммы после двойного щелчка "мышки" : оси, название, данные.

4 Технология решения задач

1-4 Этапы решения задач на ЭВМ (эл.табл.)

1. Постановка задачи: выяснение условий, оформление на листе решения разделов "дано" и "найти", заполнение таблицы начальными данными.

2. Формализация решения: составление математической модели,

3. Составление алгоритма решения

4. Оформление на листе решения формул в виде текста в разделе "математическая модель".

5. Создание сетки вычислений в разделе "решение".

6. Анализ полученных результатов

2-4 Оформление листа решения

Таблица № 2

Прочитать файл-шаблон с заданной формой листа решения или на листе создать разделы “Дано”, “Найти”, “Математическая модель”, “Решение”, "Ответ".

Назвать лист номером задачи (редактирование названия – двойной щелчок мыши на "Лист 1").

Расположить исходные данные в листе решения в разделе "Дано", указать искомые величины в разделе "Найти".

Ввести формулы( тип данных – текст) в разделе "Математическая модель" (пробел перед знаком "=").

В разделе “Решение” создать сетку вычислений в соответствии с выбранным алгоритмом:

- Обозначить искомые и промежуточные величины.

- Ввести фоpмулы (тип данных - формулы) , pеализующие метод решения.

- Выполнить копиpование данных и фоpмул, если это необходимо.

- Для графического представления результатов выделить область аргументов и функций, построить диаграмму, отредактировать диаграмму.

5 Методы решения задач

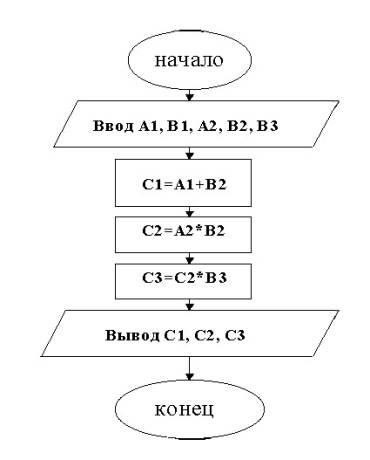
1-5 Метод последовательных вычислений

Для решения задач с последовательными действиями применяется линейный алгоритм. Рекомендуется строить на уроке блок-схемы решения задачи или упражнения в тетради, предлагать это в качестве домашнего задания. При записи алгоритма необходимо использовать имена переменных величин; для электронной таблицы именами переменных могут служить адреса ячеек.

Если искомая величина зависит от промежуточных результатов, то в формуле для искомой величины в качестве аргумента используйте имя ячейки промежуточной величины. Например, рассмотрим упражнение:

Упражнение 1

аргумент1 + аргумент2 = результат1

аргумент3 * аргумент4 = результат2

результат2 * аргумент5 = результат3

Создается сетка вычислений по схеме:

Таблица № 3

	A	B	C
1	аргумент1	аргумент2	результат1
2	аргумент3	аргумент4	результат2
3	результат2	аргумент5	результат3

В электронную таблицу вносятся данные, формулы с адресами ячеек начальных данных:

Таблица № 4

	A	B	C
1	28	127	=A1+B1
2	346	2,34	=A2*B2
3	=C2	1,57	=A3*B3

Блок-схема 1. Линейный алгоритм

Если использовать шаблон, то сетка вычислений для того же упражнения выглядит иначе:

Таблица № 5

Задача № 1

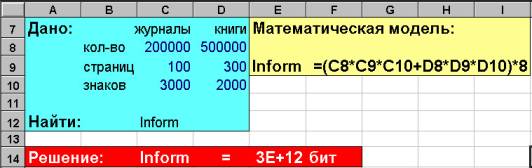
В библиотеке имеются 200 тысяч журналов по 100 страниц и по 3 тысячи знаков на странице в среднем и 500 тысяч книг по 300 страниц и по 2 тысячи знаков на странице. Вопрос: сколько информации в библиотеке ?

Таблица № 6

Для задачи №1 в разделе "Дано" начальные данные внесены как табличные, а в математической модели в качестве имен величин использованы адреса ячеек. Обозначение начальных данных должно быть понятным и соответствовать смыслу этих данных. А в формуле, конечно, нужно указывать, где брать данные, то есть адрес ячейки, где расположено число.

Задача № 2

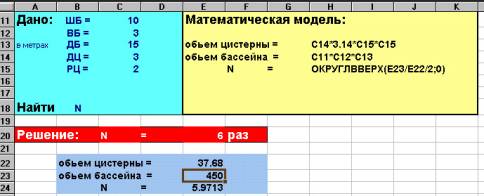
У мамы маленького великана Васи есть небольшой бассейн во дворе. Иногда Вася ходит к речке и приносит воду в бассейн в небольшой цистерне цилиндрической формы. Известны ширина ШБ, высота ВБ, длина ДБ бассейна и длина и радиус цистерны (ДЦ и РЦ). Сколько раз Васе нужно сходить к речке за водой, чтобы наполнить бассейн наполовину?

Таблица № 7

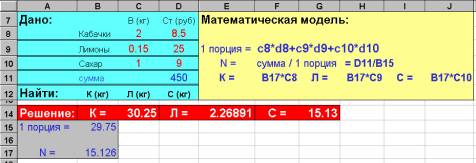
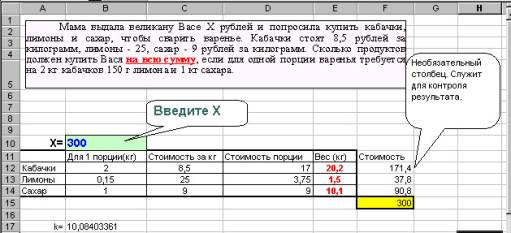
Задача № 3

Мама выдала великану Васе Х рублей и попросила купить кабачки, лимоны и сахар, чтобы сварить варенье. Кабачки стоят 8,5 рублей за килограмм, лимоны - 25, сахар - 9 рублей за килограмм. Сколько продуктов может купить Вася на всю сумму, если для одной великанской порции варенья требуется на 2 кг кабачков 150 г лимона и 1 кг сахара. Получить решение для любой суммы Х.

Таблица № 8

Таблицу можно оформить иначе, без использования шаблона.

Таблица № 9

В таблице № 9 Вы видите решение задачи № 3, но математическая модель не видна на экране. Постройте блок-схему решения. Коэффициент k показывает отличие суммарной стоимости 1 порции продуктов от имеющейся суммы.

Для самостоятельного решения:

Если в задаче сказано, что некая величина известна (например, радиус R), значит, при решении Вы самостоятельно задаёте её значение, чтобы получить численный ответ.

Задача № 4

Умная Эльза собиралась купить футболку с эмблемой за х рублей в дальнем магазине, что на у рублей дешевле, чем в ближайшем ларьке.

Но вдруг по дороге она купила книжку на сумму, в два раза большую той, которую Эльза могла сэкономить.

Вопросы:

- сколько денег потратила Эльза?

- сколько денег Эльза потратила бы, если бы она не выполнила свой план и не дошла до дальнего магазина, а воспользовалась услугами ближайшего ларька?

Задача № 5

Известно, что самая большая вершина Хибинских гор Часначорр в 6,25 раза ниже пика Победы и составляет 13,4% высоты высочайшей вершины мира Эверест. Определить высоту Часначорра, если известно, что пик Победы на 1440 м ниже Эвереста.

Задача № 6

Скорость печати у машинистки 180 знаков в минуту и рабочий день 6 часов ( в неделе 5 рабочих дней ).

Вопрос: через какой срок 10 машинисток смогут занести всю информацию, имеющуюся в библиотеке (см. задачу №1), в компьютер?

Дополнительный вопрос: можно ли использовать подобную технологию или следует поискать более эффективный способ?

Задача № 7

Две черепахи участвуют в соревновании. Первая черепаха бежала со скоростью, вдвое большей, чем у божьей коровки. У второй черепахи скорость была в полтора раза больше, чем у первой. Однако, на середине пути она перепутала направление и вернулась назад, со стартовой черты снова двинулась к финишу. Определите, кто победит, если известна скорость божьей коровки ( К см/час) и расстояние от старта до финиша (Sм).

Задача № 8

Радиус окружности, вписанной в равносторонний треугольник, равен R. Вычислить сторону, высоту и площадь треугольника.

2-5 Решение задач с условием (методика пpовеpки условия)

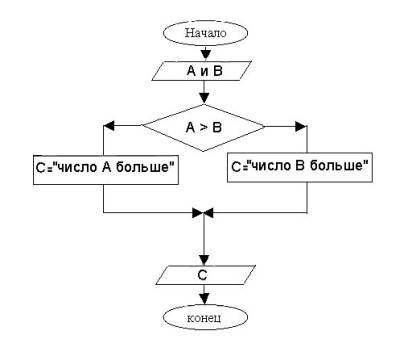
Задачи с условием решают с помощью алгоритма ветвления. Базовая алгоритмическая структура “развилка” реализуется при помощи встроенной функции
=ЕСЛИ (условие; действие1; действие2).

Условие записывают как логическое выражение. Логическое выражение может иметь значение "Истина" или "Ложь".

Условие может быть простым или сложным.

Примеры записи условия:

Таблица № 10

простое условие	сложное условие
A2>B2+36	(A1>168)*(A1<178)
C4<>36.6	(D2<КОРЕНЬ(A1))+(D2=A1)
F10=0	(A1>1)*(A1<7)+(А1=9)

Знак * означает, что обе части сложного условия должны выполняться одновременно (равносильно утверждению "и то, и другое" - логическому "и"). Знак + означает, что хотя бы одна часть сложного условия должна выполняться (равносильно утверждению "или то, или другое" - логическому "или").

Упражнение 2

Сравнить два числа А и В.

Таблица № 11

A	B	C	D	E	F	G	H
Дано:	А =	105		Решение:
	В =	93
				С =	число А больше
Найти:	С
Сравнить А и В
Математическая модель:
С	=Если(С1>С2;"число А больше";"число В больше")

Блок-схема 2. Разветвляющийся алгоритм

Упражнение 3

Вычислить арифметическое выражение (a²+d*3-b³)/(a-b)

При вычислении аpифметического выpажения с дробной частью необходимо пpовеpить знаменатель на равенство нулю:
=ЕСЛИ(a<>b;(a*a+d*3-b*b*b)/(a-b);"знаменатель pавен нулю").

Если а не равно b, то вычисляется (a²+d*3-b³)/(a-b), иначе выводим текстовое сообщение "знаменатель pавен нулю".

Таблица № 12

Дано:	a =	3	Решение:
	d =	2
	b =	3	F =	знаменатель pавен нулю
Найти:	F
F =	(a*a+d*3-b*b*b)/(a-b)
Математическая модель:
F =
ЕСЛИ(C1<>C3;(C1*C1+C2*3-C3*C3*C3)/(C1-C3); "знаменатель pавен нулю")

Задача № 9

Через иллюминатор затонувшего корабля требуется вытащить сундук с драгоценностями. Возможно ли это сделать? Выберите параметры, необходимые для решения задачи, и считайте их известными величинами.

Таблица № 13

A	B	C	D	E	F
Дано:	R=	38		Решение:
	L1=	40		Усл1 =	1
	L2=	50		Усл2 =	0
	L3=	60		Усл3 =	1
Найти:	Log			Log =	2
					сокровища можно достать
Математическая модель:
Усл1=ЕСЛИ((2*R>КОРЕНЬ(L1*L1+L2*L2));1;0)
Усл2=ЕСЛИ(2*R>КОРЕНЬ(L2*L2+L3*L3);1;0)
Усл1=ЕСЛИ(2*R>КОРЕНЬ(L1*L1+L3*L3); 1;0)
Log =	СУММ(F2:F4)
ЕСЛИ(F5=0;"сокровища недоступны";"сокровища можно достать")

Для самостоятельного решения:

Задача № 10

Решите задачу № 5 о сокровищах, используя сложное условие.

Задача № 11

Прием на работу в токарный цех авиазавода идет на конкурсной основе. Условия приема требуют 20 лет рабочего стажа и возраста не более 42 лет. Определите, кто из заданного списка конкурсантов может быть принят на работу.

Задача № 12

В школу танцев принимаются девушки и юноши, имеющие рост не ниже 168 см и не выше 178 см. Их вес должен соотноситься с ростом по формуле: значение веса < значение роста - 115. Определите, кто из списка поступающих будет принят в школу.

Задача № 13

Рис расфасован в два пакета. Вес первого - М кг, второго - N кг. Определить:

А) какой пакет тяжелее?

Б) вес более тяжелого пакета.

Задача № 14

В летний поход в школе возьмут только тех учеников, у которых оценки за четверть по математике, физике, географии и физкультуре в сумме составляют не менее 18 баллов. Определите, кто из списка желающих пойти в поход действительно может стать участником?

Задача № 15

Составить программу, по которой компьютер выполняет роль электронной няньки, заботящейся о здоровье школьника. Приводятся два варианта развития сценария, в зависимости от ответа ребенка. Нормальная температура человека: от 36.3⁰C до 36.8⁰C. И если у ребенка температура выше или ниже, то он не здоров.

1-й вариант:

Ты вчера был болен. Померь-ка температуру!

Сообщи, какая у тебя температура: 36.5

Ты здоров, дружок! Можешь идти в школу.

Желаю успехов!

2-й вариант:

Ты вчера был болен. Померь-ка температуру!

Сообщи, какая у тебя температура: 37.7

Ты еще болен! Раздевайся и ложись в постель.

Поправляйся, дружок!

Задача № 16

Составить программу, по которой компьютер выполняет роль электронной няньки, заботящейся о здоровье школьника. Приводятся два варианта развития сценария, в зависимости от ответа ребенка. Нормальная температура воздуха, при которой дети посещают школу не ниже -23⁰C.

1-й вариант:

Вчера был сильный мороз. Посмотри на термометр сегодня.

Сообщи, какая температура воздуха сейчас: –10

Дружок! Можешь идти в школу.

Желаю успехов!

2-й вариант:

Вчера был сильный мороз. Посмотри на термометр сегодня.

Сообщи, какая температура воздуха сейчас: –40

Занятия в школе отменяются!

Выходить на улицу опасно для твоего здоровья!

3-5 Решение задач с повторяющимися действиями

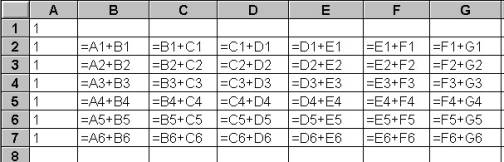
* Копирование формул

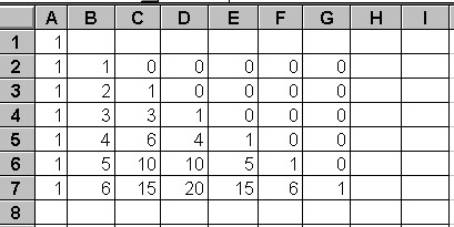
Если в задаче нужно выполнить несколько похожих действий, то используем циклический алгоритм. Решение задач с повторяющимися действиями в электронных таблицах выглядит несколько проще, чем на языке программирования. Для реализации циклических действий нужно применить копирование формул.

Упражнение 4

Построить числовую пирамиду "треугольник Паскаля". Заполните столбец А. В ячейку В2 запишите формулу, скопируйте формулу в остальные ячейки.

Таблица № 14

Получите числовую зависимость (см. таблицу № 15)

Таблица № 15

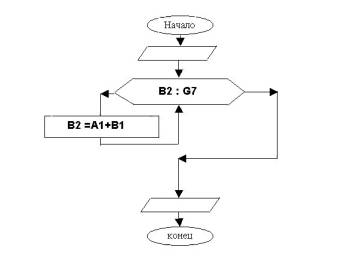
Алгоритм для выполнения упражнения 4 мы изобразили в блок-схеме 3. Описание действий не является строгим и требует пояснения. В блоке, описывающем количество повторяющихся действий, указан диапазон ячеек, в которые надо скопировать формулу. Сама формула сначала записывается в ячейку В2 электронной таблицы. В блок-схеме она находится в блоке, описывающем то действие, которое должно повторяться известное количество раз.

блок-схема 3. Циклический алгоритм

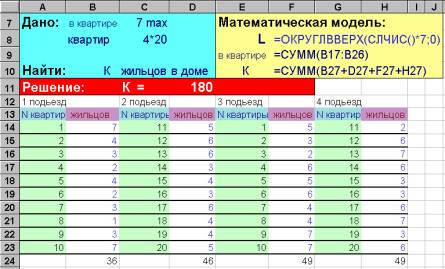
Задача № 17

В доме 4 подьезда, в каждом подьезде 20 квартир. В квартире живет от 1 до 7 человек. Подсчитать количество жильцов в каждом подьезде и в доме. (Для каждой квартиры количество жильцов задайте случайным образом)

Таблица № 16

Для самостоятельного решения:

Упражнение 5

Напечатайте таблицу перевода температуры из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) для значений температуры от 15⁰ С до 30⁰ С с шагом 1⁰ С. Формула перевода из градусов по шкале Цельсия (С) в градусы по шкале Фаренгейта (F) F=1.8*C+32

Упражнение 6

Напечатайте таблицу перевода миль в километры для расстояний от 5 до 75 миль с шагом 5 миль, если 1 морская (английская) миля составляет 1.852 км.

Упражнение 7

Напечатайте таблицу перевода расстояний в дюймах в сантиметры для значений от 1 до 10 дюймов с шагом 1 дюйм, если 1 дюйм=2.54 см.

Упражнение 8

Напечатайте таблицу соответствия между весом в фунтах и весом в килограммах для значений от 1 до 10 фунтов с шагом 1 фунт, если 1ф=454 г.

Задача № 18

Составьте таблицу - календарь на месяц с указанием дней недели, с подсчетом количества рабочих дней. Выходным считать воскресенье.

Задача № 19

Маленький великан Вася выpастает на 1 сантиметp в день. Его pост в день М pавен одному метpу. Мама великанша измеpяет pост сына каждую неделю и записывает в книжечку.

Выведите на экpан записи из маминой книжечки за 20 недель после дня М.

Задача № 20

Маленький великан Вася с каждой неделей может поднимать на 5 килограмм больше, чем в предшествующую неделю. В день М он поднимал 230 килограммов. Сколько дней назад родился Вася, если в первый день своей жизни он ничего не мог поднять? Сколько килограмм он сможет поднять в свой первый день рождения? Какой вес он поднимет от дня М до первого дня рождения (1 год) в сумме, если будет упражняться раз в неделю и записывать результат? Как увидеть на экране Васины записи?

Задача № 21

В день М мама подарила маленькому великану Васе копилку, в которой лежал 1 рубль и стала давать ему каждый день по 3 копейки. Выведите на экран сумму, лежащую в копилке в конце каждой недели в течении 15 недель.

Задача № 22

В сосуде, объём которого равен V₀ литров, содержится р%-ный раствор соли. Из сосуда выливается А литров смеси и доливается А литров воды, после чего раствор перемешивается. Эта процедура повторяется N раз. Какова будет концентрация соли после N процедур? Решите задачу для N = 3, N = 6, N = 12, N = 30.

Задача № 23

Поезд должен пройти 100 км за 2 часа. По дороге расположены 7 станций. Выяснить, сколько минут сможет стоять поезд на каждой станции, если его средняя скорость на всех участках пути (исключая остановки) будет составлять в час: 200 км, или 100 км, или 80 км, или 60 км, или 50 км, или 40 км. Время остановки одинаково на всех станциях.

* Функциональные зависимости.

"Если Вы составили систему уравнений, мы Вам ее решим."

Горстко А.Б.

Многие задачи сводятся к решению уравнения f(x)=0. Более сложные задачи решаются с помощью системы таких уравнений или неравенств.

Задача № 24

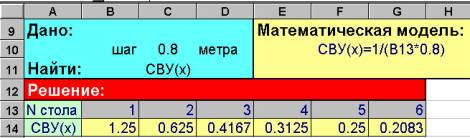
Сила воздействия учителя СВУ на ученика зависит от расстояния Х между учителем и учеником и выражается функцией СВУ(X)=1/Х. Вычислите значение СВУ для учеников, которые сидят в классе за 1 столом, за 2, за 3, 4, 5 и за 6 столом. Расстояние между рядами столов и между учителем и 1 столом считать одинаковым и равным 80 см. Если СВУ меньше 0.25, то знания ученика не достигают и оценки 3. Сколько рядов столов можно ставить в классе, чтобы при этом не было двоечников?

Очевидно, что для решения задачи нужно построить таблицу значений функции СВУ(Х) для различных значений аргумента Х. Таблица № 19 с решением на странице . Такой метод решения задач называется методом табулирования функции. Рассмотрим его подробнее.

* Метод табулирования функций.

Для решения уравнения у(х) = 0 построим таблицу значений x и y(x) на заданном промежутке для х:

Таблица № 17

х	y(х)
х1	y1
......	......
xi	yi
......	......
хn	yn

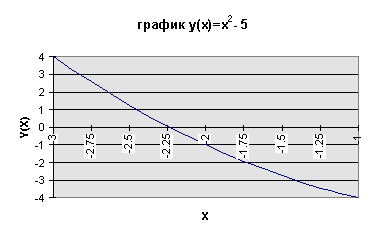
найдем наиболее близкое к нулю значение yi, и соответствующее значение х примем за приближенное решение уравнения.

Упражнение 9

Построить таблицу расчета значений функции у(х) = х² – 5 для интервала [-3;-1 ] с точностью 0,25. Найти решение уравнения
х² – 5 = 0

Таблица № 18

х	у(х)
-3	4
-2.75	2.5625
-2.5	1.25
-2.25	0.0625
-2	-1
-1.75	-1.9375
-1.5	-2.75
-1.25	-3.4375
-1	-4

Наиболее близкое к нулю значение у = 0.0625, соответствующее значение
х = -2.25 и есть искомое решение уравнения.

А теперь рассмотрим решение задачи № 24.

Расстояние Х вычисляется по формуле 0.8*N стола. Формула для вычисления СВУ(Х) из ячейки В14 копируется в С14, D14 и далее.

Таблица № 19

Из таблицы видно, что нельзя ставить в классе столы более чем в 5 рядов.

Для самостоятельного решения:

Упражнение 10

Построить таблицу расчета значений функции у(х) = –х² + 5 для интервала [ 0; 4 ] с шагом 0,5. Найти решение уравнения –х² + 5 = 0

Упражнение 11

Построить таблицу расчета значений функции у(х) = 2 * х² – 5 для интервала [-3; 0 ] с шагом 0,25. Найти решение уравнения 2 * х² – 5 = 0

* Графический метод.

По построенной таблице значений аргумента и функции (х и у) построим линейный график (используем мастер диаграмм), найдем точку пересечения графика функции и оси Ох.

Диаграмма 1

На диаграмме 1 решение упражнения 9. Мы получаем тот же ответ
х = -2.25, но увидеть его на графике легче, чем в таблице.

Для уравнений вида y1(x) = y2 (x) или системы двух уравнений

y1(x) = 0

y2(x) = 0

решение можно получить двумя способами:

1) построим два графика y1(x) = 0 и y2(x) = 0 и найдем точку их пересечения,

2) построим график функции f(x) = y1 – y2 (предварительно дополним таблицу столбиком значений y1–y2 и найдем решение для уравнения f (x) = 0 (точку пересечения графика с осью Ох).

Задача № 25

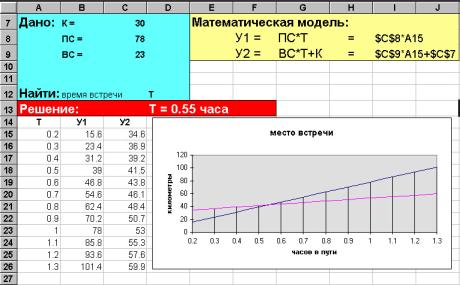
Два автомобиля выехали одновременно по одной дороге в одном направлении из разных городов, Солнечное и Мокрое. Между этими городами К километров. Первый автомобиль едет со скоростью ПС км/час, второй - со скоростью ВС км/час. Определите, встретятся ли они на дороге, если да, то через сколько часов?

Таблица № 20

Получен ответ Т = 0.55, это значение определено визуально по графику и соответствует значению Т в точке пересечения графиков функций У1 и У2.

Для самостоятельного решения:

Упражнение 12

Решите систему уравнений:

3 * Х + 5 = 0 (У1)

Х² / 3 - 10 = 0 (У2)

Задача № 26

Решите задачу № 5 ( о высоте горы Часначорр) графическим методом.

* Метод итераций.

Решение уравнения не всегда бывает целым числом. Часто в результате получаем число с бесконечным количеством цифр после запятой. Чтобы не считать все эти цифры (а это занятие бессмысленное), задается число верных знаков, которые необходимо найти. Существует понятие точности решения уравнения. Например, проверяя функцию у(х) = х² – 5 для интервала [-3;-1 ] с шагом 0.25, мы получили ответ 2.25. Точность этого решения при графическом методе можно принять за 0.1, при методе табулирования точность не превышает 0.2. Таким образом, ответ правильней записать как равный 2.2.

Если полученный результат не удовлетворяет заданной точности решения уравнения, то можно применить последовательные приближения (метод итераций):

1. выбрать два значения х( i-1) и x( i+1) аргумента Х, ограничивающие отрезок, на котором лежит найденное приближенное значение y( i ).

2. Вычислить новый шаг для таблицы, по которой уже построен график функции у(х), по формуле:

H = [х( i+1) - x( i-1)] / n

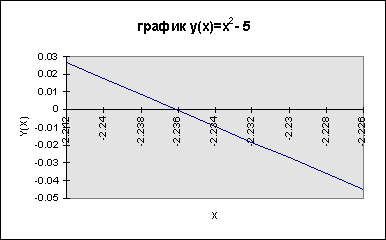
3. В ячейке, где находилось значение х(1), разместить значение
x( i-1), в ячейке, где находилось значение х(2), разместить значение x( i-1)+Н, выделить эти две ячейки и применить пошаговое копирование для остальных ячеек значений аргумента Х.

4. На графике найти точку пересечения с осью Х (близкое к нулю значение yi ) и значение х принять за приближенное решение уравнения.

5. Если точность решения снова недостаточна, повторить шаги1-4.

Упражнение 13

Найти решение уравнения у(х) = х² – 5 = 0 для интервала [-3;-1 ] с точностью 0.001.

Повторим несколько раз итерационную процедуру, получим таблицу и график, ответ х = -2.236

Таблица № 21

х	у(х)
-2.242	0.026564
-2.24	0.0176
-2.238	0.008644
-2.236	-0.0003
-2.234	-0.00924
-2.232	-0.01818
-2.23	-0.0271
-2.228	-0.03602
-2.226	-0.04492

Диаграмма 2

Для самостоятельного решения:

Упражнение 14

Найдите решение уравнения 3*х² +2*x - 4 = 0 на интервале [ 0; 2] с точностью 0.001

4-5 Решение задач обработки множеств

С помощью электpонных таблиц можно решать задачи обработки множеств (наборов данных одного типа). Такого рода задачи в программировании решаются с помощью специальной структуры данных – "массив". Стpуктуpа электpонной таблицы позволяет наглядно pаботать с массивами. Пpимеpом одномеpных массивов могут служить стpоки и столбцы, заполненные однотипными данными. Аналогом двумеpного массива является "пpямоугольная" часть электpонной таблицы, которая определяется заданным диапазоном (А4:В18 или А10:С15). Их можно обрабатывать аналогичным образом, используя те же алгоритмы, что и в программировании, или стандартные функции "Excel".

Перечислим операции, которые чаще всего проводятся с множествами и для некоторых операций укажем средство выполнения:

· соpтиpовка элементов множества по возpастанию и убыванию (меню "Данные", "Сортировка");

· подсчёт суммы элементов множества (функция СУММ(<диапазон>));

· умножение элементов множества на число (формула =А1*К);

· замена элементов множества по условию (функция ЕСЛИ);

· преобразование одного множества в другое по условию (функция ЕСЛИ);

· подсчёт количества элементов множества, попадающих в заданный интеpвал;

· нахождение максимума и минимума в множестве (функции МАКС и МИН);

· перестановка элементов множества по заданному правилу;

· операции с матрицами и векторами (инвеpтиpование матpицы; умножение вектоpа на число).

Упражнение 15

Дано множество чисел 12, 1, 0, -5, 3, 4, 0. Заменить нулевые значения на 7.

Таблица № 22

A	B	C	D	E	F	G
Дано:				Решение:	12	12
Дан массив 12, 1, 0, -5, 3, 4, 0.					1	1
					0	7
Найти:					-5	-5
Заменить нулевые значения					3	3
массива на 7.					4	4
Математическая модель:					0	7
G1	=ЕСЛИ(F1=0;7;F1)

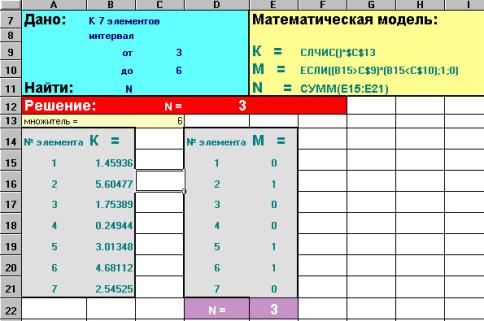
Упражнение 16

Дано множество чисел. Подсчитать количество чисел, попадающих в заданный интервал.

Таблица № 23

Чтобы выбpать числа из множества случайных чисел, удовлетворяющих условию, достаточно набpать фоpмулу в соседней ячейке:
=ЕСЛИ((B16>C$9)*(B16<C$10);1;0)
и скопиpовать эту фоpмулу для каждого числа (в столбце Е в нашем примере). Получим значение 1 для чисел, попадающих в заданный интервал. Далее следует сложить все полученные значения.

=СУММ(E15:E21)

Задача № 27

У маленького великана Васи 40 двоюродных братьев. Самый высокий из них ростом 1 метр. Если сложить рост всех братьев, то полученная сумма как раз равна росту Васи. Получите значение его роста, если задать рост братьев случайным образом.

Таблица № 24

Дано:		К - 40 элементов			Математическая модель:
		K(max)=100 см
		Р=СУММ(К)				К =			ОКРУГЛ(СЛЧИС()*100;0)
Найти:		Р			Р =			СУММ(B19:E28)/100
Решение:
К, рост сорока братьев, в см							Р, рост Васи, в метрах
38	83		44	66
69	60		96	17				Р =		19,81
25	88		8	4
29	4		81	72
30	63		72	20
81	37		35	93
43	1		5	56
46	25		42	91
88	22		67	28
78	17		65	92

Для самостоятельного решения:

Задача 28

Изменить в таблице количество жильцов каждой квартиры подъезда, если жильцы поменяли квартиры так, что все, кто жил в нечетных квартирах, стали жить в четных. (см. задачу № 16)

6 Приложение 1. Встроенные функции “MS Excel 7.0”

ЕСЛИ (условие; действие1; действие2) - логическая, проверка условия

СУММ(<диапазон ячеек>) - математическая, сумма чисел

КОРЕНЬ(<число или выражение>) - математическая, квадратный корень числа

СЛЧИС()- математическая, дает число от 0 до 1

ФАКТР(<число или выражение>) - математическая, считает факториал числа

ОКРУГЛВВЕРХ(<число или выражение>;0) - математическая

СРЗНАЧ(<диапазон ячеек>) - статистическая, среднее значение

МИН(<диапазон ячеек>) - статистическая, минимальное значение

МАКС(<диапазон ячеек>) - статистическая, максимальное значение

** Чтобы увидеть полный список функций, включите мастер функций в Excel.

7 Приложение 2. Примерное тематическое планирование, раздел "Алгоритмы решения задач в электронных таблицах "Excel"

учитель Мартыненко О.В., 8 класс, 40 часов

№ урока	Тема урока
1-2	Алгоритмы. Свойства алгоритмов
3-4	Электронная таблица. Расчет по формулам. Этапы решения задач на ЭВМ
5-6	Приемы редактирования. Построение числовых пирамид
7-8	Форматирование ячеек. Построение диаграмм
9-10	Формализация решения задачи. Оформление листа решения.
11-12	Метод последовательных вычислений. Практикум решения задач.
13-14	Метод последовательных вычислений. Встроенные функции
15-16	Метод проверки условия. Функция «ЕСЛИ»
17-18	Практикум решения задач. Задачи с условиями
19-20	Решение задач с повторяющимися действиями.
21-22	Реализация циклического алгоритма.
23-24	Функциональные зависимости. Метод табулирования функции
25-26	Графический метод. Метод итераций
27-28	Обработка множества элементов таблицы
29-30	Практикум «решение задач»
31-32	Контрольная работа
33-34	Построение и использование вспомогательных алгоритмов
35-36	Практикум решения комбинированных задач
37-38	Расширенные возможности электронной таблицы.
39-40	Контрольная работа

8 Литература

1. Бешенков С.А., Гейн А.Г., Григорьев С.Г. “Информатика и информационные технологии”, УГПУ, Екатеринбург, 1995

2. Гарнаев А. «Использование MS Excel и VBA в экономике и финансах», bhv, 1999

3. Горстко А.Б., Чердынцева М.И. "Информатика для школьников и всех-всех-всех", Ростов-на-Дону, "Феникс", 1996

4. Зайцева В.П., “Вычислительный эксперимент на уроке”:В сб. “Информатика-97”, Мурманск, 1997

5. Зайцева В.П., “Электронные таблицы на уроке”, Мурманск, 1997

6. Зайцева В.П., Паялов А.В., “В помощь учителю. Задачи по теме моделирование”, Мурманск, !999

7. Курицкий Б.Я., “Поиск оптимальных решений средствами Excel 7.0”, СПб, “BHV - Санкт-Петербург”, 1997

8. Лапчик М.П., “Вычисления. Алгоритмизация. Программирование.”, М., “Просвещение”, 1988

9. Лурье М.А., Александров Б.И., “Задачи на составление уравнений”, М., “Наука”, 1976

10.Очков В., “Excel 5.0: заметки на полях”, "Компьютер пресс" №3 1995, стр.44

11.Пак Н.И., “Компьютерное моделирование”, TV-info, 1996

Photoshop

Word

Excel

Pascal

HTML

Access

Разное

Вернуться

---